Bayer Bäume
1.3 Löschen aus Bayer-Bäumen
Das Einfügen ist nur eine der beiden benötigten Operationen. Natürlich sollten Daten auch wieder gelöscht werden können. Jedoch ist das Löschen aus B-Bäumen noch ein wenig aufwendiger.
Fall 1.1
Das zu löschende Element befindet sich in einem Blatt. Dieses Blatt enthält mehr als k Daten. In diesem Fall kann das Element einfach gelöscht werden, ohne den Baum zu reorganisieren. Der modifizierte Baum genügt wieder den
B-Baum-Eigenschaften.
Fall 1.2
Enthält das Blatt jedoch genau k Elemente, entsteht durch das Löschen ein Unterlauf. Denn jeder Knoten eines B-Baumes muß mindestens k Elemente enthalten. Was bei einem Unterlauf getan werden muß, dürfte klar sein:
Von irgendwoher müssen Elemente genommen werden, um das entsprechende Blatt aufzufüllen. Die B-Baum-Eigenschaften besagen ja, daß jedes Blatt außer
der Wurzel mindestens k Elemente enthält. Es ist naheliegend, diese zusätzlichen Elemente von einem Nachbarknoten zu nehmen.
Hier liegt aber auch gleich das Problem : Wenn der Nachbarknoten nur k Elemente hat, kann dieser keine an den Knoten mit dem Unterlauf abgeben.
Fall 1.2 a
Zunächst soll der Nachbarknoten mehr als k Elemente besitzen. Jetzt können Elemente wie Perlen an einer Kette vom linken Knoten über den gemeinsamen Vaterknoten zum rechten Knoten fließen. Dieser Vorgang wird solange wiederholt, bis beide Knoten ausgeglichen sind. Deswegen nennt man diese Methode auch
"Löschen durch Ausgleichen" (Abb. 4). Sie stört die lexikografische Ordnung nicht, und es entsteht wieder ein B-Baum, der den B-Baum-Eigenschaften entspricht.
Fall 1.2 b
Das obenerwähnte Verfahren schlägt natürlich fehl, wenn der Nachbarknoten selber nur k Elemente besitzt. In diesem Fall werden beide Knoten zu einem einzigen Knoten verschmolzen. Das Element "b" des Vaterknotens nimmt man ebenfalls in den neuentstehenden Knoten auf, und es entsteht ein Blatt, mit genau 2 * k
Elementen. Dieser Vorgang wird mit "Löschen durch Mischen bezeichnet" (Abb. 5); der Mischvorgang ist das genaue Gegenstück zum Teilungsprozeß beim Einfügen. Da der Mischvorgang dem Vaterknoten das Element "b" entzieht, muß es dort gelöscht werden. Wiederum entsteht ein rekursiver Prozeß, der sich schlimmstenfalls bis zur Wurzel fortsetzt.
Anmerkung
Ist der Knoten, aus dem gelöscht werden soll, der äußerst linke Knoten, so wird als Knoten für den Ausgleich bzw. für das Mischen der rechte Nachbar herangezogen. Ist der Knoten, aus dem gelöscht werden soll, der äußerst rechte Knoten so ist es genau umgekehrt. Das hat zur Folge, daß je nach Position des Knotens, aus dem gelöscht werden soll, die Elemente zum Ausgleich bzw. zum Mischen aus dem entsprechenden Nachbarknoten genommen werden müssen.
Fall 2
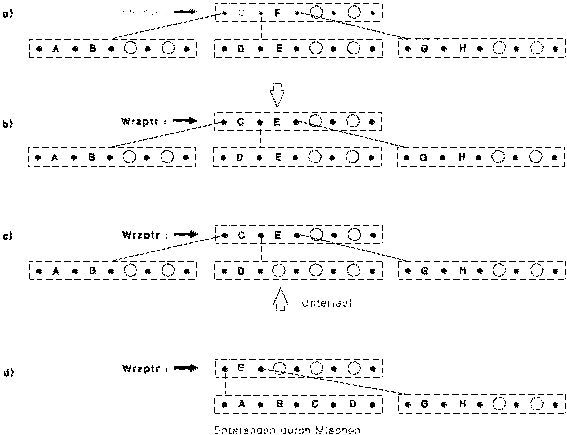
Das zu löschende Element befindet sich nicht in einem Blatt, sondern in einem inneren Konten. Hier scheint der Reorganisationsaufwand besonders groß zu sein, da durch das Löschen ein Loch entstehen würde. Die Teilbäume darf man natürlich nicht mitlöschen (wie z.B. "G" und "H" beim Löschen von "F").
Glücklicherweise gibt es für diesen Fall einen einfachen Trick:
Das zu löschende Element wird durch das größte Datum im linken Teilbaum (direkter linker Nachbar) ersetzt. Anschließend kann dann dieses größte Element normal gelöscht werden, da es sich immer auf einem Blatt befindet (das größte Element in einem Baum oder Teilbaum befindet sich immer in einem Blatt !).
Dieser kleine Trick reduziert das Problem des Löschens von inneren Elementen auf das Löschen in Blättern. In Abb. 6 wird "F" erst durch "E" ersetzt, was die lexikografische Ordnung nicht verletzt und dann das Element "E" im linken Teilbaum gelöscht.
1.4 Logischer Aufbau einer Implementierung
Beschreibung der B-Baum-Struktur1
Sei k wieder eine ganze Zahl k > 0. Der implementierte B-Baum ist entweder leer oder ein geordneter Baum mit Folgenden Eigenschaften:
- Jeder Pfad von der Wurzel zu einem Blatt hat die gleiche Länge.
- Jeder Knoten hat mindestens 2 Nachfolger. Die Wurzel ist ein Blatt oder hat mindestens 2 Nachfolger.
- Jeder Knoten hat höchstens 2 * k Nachfolger.
- Jedes Blatt hat mindestens 1 und höchstens 2 * k Elemente.
- Wird ein neuer Knoten (Blatt) durch Splitting erzeugt, so enthält der eine Knoten k und der andere k + 1 Daten.
- Ein Knoten wird dann gelöscht, wenn sein letztes Element gelöscht wird.
- Daten sind nur in den Blättern gespeichert.
- Innere Knoten enthalten die größten Schlüssel ihrer Teilbäume.
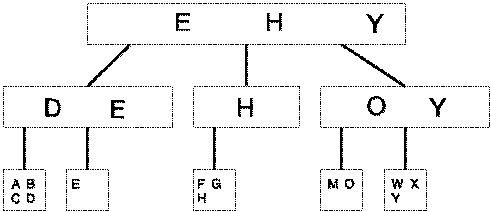
Das Einfügen ist nur eine der beiden benötigten Operationen. Natürlich sollten Daten auch wieder gelöscht werden können. Jedoch ist das Löschen aus B-Bäumen noch ein wenig aufwendiger.
Fall 1.1
Das zu löschende Element befindet sich in einem Blatt. Dieses Blatt enthält mehr als k Daten. In diesem Fall kann das Element einfach gelöscht werden, ohne den Baum zu reorganisieren. Der modifizierte Baum genügt wieder den
B-Baum-Eigenschaften.
Fall 1.2
Enthält das Blatt jedoch genau k Elemente, entsteht durch das Löschen ein Unterlauf. Denn jeder Knoten eines B-Baumes muß mindestens k Elemente enthalten. Was bei einem Unterlauf getan werden muß, dürfte klar sein:
Von irgendwoher müssen Elemente genommen werden, um das entsprechende Blatt aufzufüllen. Die B-Baum-Eigenschaften besagen ja, daß jedes Blatt außer
der Wurzel mindestens k Elemente enthält. Es ist naheliegend, diese zusätzlichen Elemente von einem Nachbarknoten zu nehmen.
Hier liegt aber auch gleich das Problem : Wenn der Nachbarknoten nur k Elemente hat, kann dieser keine an den Knoten mit dem Unterlauf abgeben.
Fall 1.2 a
Zunächst soll der Nachbarknoten mehr als k Elemente besitzen. Jetzt können Elemente wie Perlen an einer Kette vom linken Knoten über den gemeinsamen Vaterknoten zum rechten Knoten fließen. Dieser Vorgang wird solange wiederholt, bis beide Knoten ausgeglichen sind. Deswegen nennt man diese Methode auch
"Löschen durch Ausgleichen" (Abb. 4). Sie stört die lexikografische Ordnung nicht, und es entsteht wieder ein B-Baum, der den B-Baum-Eigenschaften entspricht.
Fall 1.2 b
Das obenerwähnte Verfahren schlägt natürlich fehl, wenn der Nachbarknoten selber nur k Elemente besitzt. In diesem Fall werden beide Knoten zu einem einzigen Knoten verschmolzen. Das Element "b" des Vaterknotens nimmt man ebenfalls in den neuentstehenden Knoten auf, und es entsteht ein Blatt, mit genau 2 * k
Elementen. Dieser Vorgang wird mit "Löschen durch Mischen bezeichnet" (Abb. 5); der Mischvorgang ist das genaue Gegenstück zum Teilungsprozeß beim Einfügen. Da der Mischvorgang dem Vaterknoten das Element "b" entzieht, muß es dort gelöscht werden. Wiederum entsteht ein rekursiver Prozeß, der sich schlimmstenfalls bis zur Wurzel fortsetzt.
Anmerkung
Ist der Knoten, aus dem gelöscht werden soll, der äußerst linke Knoten, so wird als Knoten für den Ausgleich bzw. für das Mischen der rechte Nachbar herangezogen. Ist der Knoten, aus dem gelöscht werden soll, der äußerst rechte Knoten so ist es genau umgekehrt. Das hat zur Folge, daß je nach Position des Knotens, aus dem gelöscht werden soll, die Elemente zum Ausgleich bzw. zum Mischen aus dem entsprechenden Nachbarknoten genommen werden müssen.
Fall 2
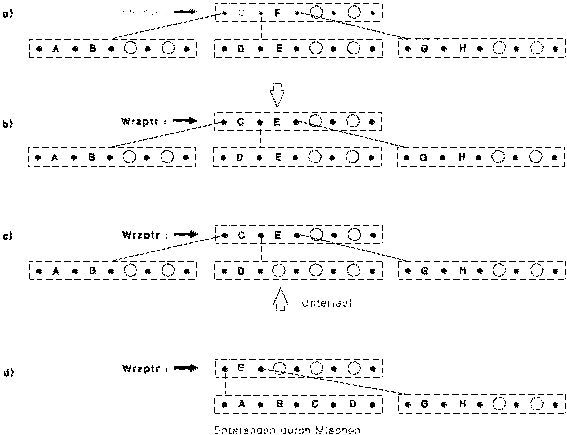
Das zu löschende Element befindet sich nicht in einem Blatt, sondern in einem inneren Konten. Hier scheint der Reorganisationsaufwand besonders groß zu sein, da durch das Löschen ein Loch entstehen würde. Die Teilbäume darf man natürlich nicht mitlöschen (wie z.B. "G" und "H" beim Löschen von "F").
Glücklicherweise gibt es für diesen Fall einen einfachen Trick:
Das zu löschende Element wird durch das größte Datum im linken Teilbaum (direkter linker Nachbar) ersetzt. Anschließend kann dann dieses größte Element normal gelöscht werden, da es sich immer auf einem Blatt befindet (das größte Element in einem Baum oder Teilbaum befindet sich immer in einem Blatt !).
Dieser kleine Trick reduziert das Problem des Löschens von inneren Elementen auf das Löschen in Blättern. In Abb. 6 wird "F" erst durch "E" ersetzt, was die lexikografische Ordnung nicht verletzt und dann das Element "E" im linken Teilbaum gelöscht.
1.4 Logischer Aufbau einer Implementierung
Beschreibung der B-Baum-Struktur1
Sei k wieder eine ganze Zahl k > 0. Der implementierte B-Baum ist entweder leer oder ein geordneter Baum mit Folgenden Eigenschaften:
- Jeder Pfad von der Wurzel zu einem Blatt hat die gleiche Länge.
- Jeder Knoten hat mindestens 2 Nachfolger. Die Wurzel ist ein Blatt oder hat mindestens 2 Nachfolger.
- Jeder Knoten hat höchstens 2 * k Nachfolger.
- Jedes Blatt hat mindestens 1 und höchstens 2 * k Elemente.
- Wird ein neuer Knoten (Blatt) durch Splitting erzeugt, so enthält der eine Knoten k und der andere k + 1 Daten.
- Ein Knoten wird dann gelöscht, wenn sein letztes Element gelöscht wird.
- Daten sind nur in den Blättern gespeichert.
- Innere Knoten enthalten die größten Schlüssel ihrer Teilbäume.

 Deutsch
Deutsch Österreich
Österreich Italiano
Italiano English
English Français
Français Español
Español Nederlands
Nederlands Português
Português Polski
Polski



