Bayer Bäume

1.5 Vergleich und Besonderheiten : Implementierung / Bayer-Baum

Da die Ordnung k eines B-Baumes normalerweise etwa zwischen 100 und 200 liegt, geht dadurch, daß die Daten nur in den Blättern gespeichert sind, nicht wesentlich viel an Speicherplatz verloren.



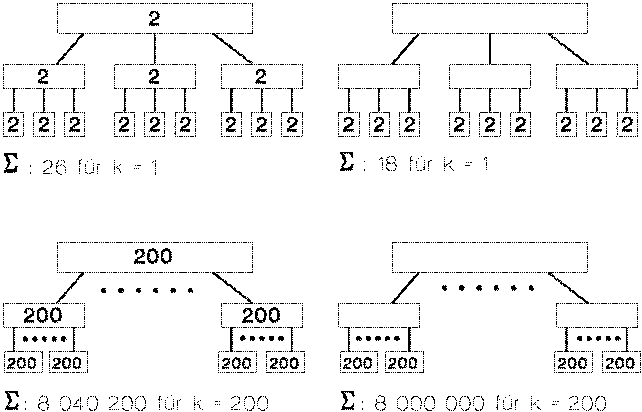
Für k = 1 hat der B-Baum etwa 45 % mehr Speicherkapazität als die Implementierung (26 / 18 * 100 % - 100 %). Für k = 200 hat der B-Baum nur noch 0.5 % (8 040 200 / 8 000 000) mehr Kapazität als die Implementierung. Man kann also davon ausgehen, daß mit steigendem k die Implementierung den originalen
B-Baum aproximiert. Das Beispiel zeigt, daß man bei einem normalen k von 200 eine fast optimale Annäherung der Speicherkapazität erreicht. B-Bäume werden normalerweise für große Datenmengen eingesetzt, insofern kann man davon ausgehen, daß der B-Baum und die Implementierung in Bezug auf die Speicher-kapazität gleichwertig sind.

Suchen bei der Implementierung

Im wesentlichen funktioniert das Suchen genauso wie bei einem normalen B-Baum. Jedoch muß man immer den gesamten Weg von der Wurzel bis zum Blatt absuchen. Aus Abb. 8 ist jedoch zu erkennen, daß B-Bäume besonders niedrig sind, sodaß dieser Nachteil nicht besonders ins Gewicht fällt.

Einfügen bei der Implementierung

Auch hier werden die Daten nur in die Blättern eingefügt. Eine Reorganisation muß nur dann durchgeführt werden, wenn der einzufügende Schlüssel größer ist als der größte Schlüssel im Teilbaum. Die Reorganisation wird dann rekursiv von dem entsprechenden Blatt bis zur Wurzel des entsprechenden Teilbaums durchgeführt. Bei einem Splitting wird in der darüberliegenden Stufe einfach nur der entsprechende Schlüssel eingefügt. Auch hier ergibt sich - wie auch beim originalen B-Baum - eventuell die entsprechende Reorganisation.

Löschen bei der Implementierung

Hier ergibt sich ein wesentlicher Vorteil der Implementierung gegenüber dem
B-Baum, da sich bei der Implementierung das Löschen nur auf die Blätter bezieht.
Eine Reorganisation muß nur dann durchgeführt werden, wenn das größte Element in einem Knoten gelöscht werden soll.Auch jetzt setzt sich die Reorganisation entsprechend weit nach oben fort, bis der entsprechende Schlüssel überall geändert ist. Ein Mischen oder Ausgleichen gibt es bei der Implementierung nicht. Die Knoten bleiben solange erhalten, bis ihr letztes Element gelöscht wird. Erst jetzt wird der entsprechende Platz an die Freispeicherverwaltung zurückgegeben. Der Vorteil liegt hier ganz klar beim geringen Reorganisationsaufwand. Der Nachteil, der sich vielleicht daraus ergeben könnte, ist daß man immer eine gewisse Anzahl von relativ leeren Knoten in der Datei hat, was auf jeden Fall einen Geschwindigkeitsvorteil mit sich bringt. Denn beim Einfügen in diese Knoten muß nur reorganisiert werden, wenn sich der größte Schlüssel ändert (für diese Knoten entfällt das Splitting). Normalerweise hält man Index und Daten voneinander getrennt, insofern wirkt sich die Anzahl dieser Knoten nur auf den Index aus. Wie schon erwähnt sind B-Baum-Dateien groß, sodaß die Anzahl der relativ leeren Knoten höchstens einen kleinen Prozentsatz ausmacht und somit vernachlässigt werden kann.

1.6 Verbesserungen

Index- und Datendatei

Man sollte immer mit einem getrennten Indexbereich (Indexdatei) und einem getrennten Datenbereich (Datendatei) arbeiten. Das Datenverwaltungssystem (DVS) greift nicht auf Datensätze, sondern nur auf Blöcke zu. Im BS 2000 ist die kleinste Blockeinheit eine PAM-Seite = 2 KB, und unter MS-DOS ist die kleinste Clustereinheit für HDs = 2 KB (für FDs 512 Bytes). Die dem Index zugrundeliegende
logische Blockgröße sollte im Overhead des Indexes gespeichert werden, wodurch eine Konvertierung in andere logische Blockgrößen leicht möglich wird. Die logische Blockgröße sollte immer ein ganzzahliges Vielfaches der physikalischen Speichereinheit sein, und logische sowie physikalische Blockgrenzen sollten in jedem Fall aufeinanderfallen. Nur so ist es möglich, einen logischen Block mit einem Hintergrundspeicherzugriff in den Hauptspeicher zu laden.

Beispiel : Annahme man legt den Wurzelblock unter MS-DOS in einer Datei ab Offset 200 ab, so muß das System Cluster 0 und Cluster 1 (zwei
Zugriffe) laden, damit die Wurzel (2 KB) in den Hauptspeicher gelangt.

Geht man von einer durchschnittlichen Schlüssellänge von 10 bis 20 Zeichen aus und rechnet den Platz für die entsprechenden Pointer dazu, so kann man in einem 2 KB Block ungefähr 100 bis 150 Elemente unterbringen.

Hält man Daten und Index vermischt, so ist dieses blockweise Laden nicht mehr möglich, da die Datensätze verschiedene Länge haben können (nur die Schlüssel müssen gleich lang sein) oder Datensätze über Blockgrenzen hinausgehen. In jedem Fall ist ein Datensatz mit seinen Daten länger als der Schlüssel selbst, wodurch bei vermischter Organisation weniger Elemente in einen Knoten passen. Das hat zur Folge, daß der B-Baum schneller in die Tiefe geht und zum Auffinden eines Datums somit mehr Speicherzugriffe erforderlich sind.

Hält man Index- und Datendatei getrennt, so kann man die Datensätze in der Datendatei mit und ohne Schlüssel speichern. Zusätzliches Speichern der Schlüssel in der Datendatei vergrößert diese nur geringfügig, da die Schlüssellänge normalerweise relativ klein gegenüber der Datensatzlänge ist.
Für den Fall, daß der Index aus irgendwelchen Gründen zerstört wird, ist er somit aus der Datendatei rekonstruierbar, was zur Datensicherheit beiträgt.

Knoten im RAM halten

Eine weiteren Geschwindigkeitsvorteil erhält man dadurch, daß man den Wurzelknoten (oder ganze Stufen) im RAM hält. Man spart somit bei jedem Suchen, Einfügen und Löschen einen Hintergrundspeicherzugriff, was einer Geschwindigkeitszunahme von 20 bis 30 % entspricht, denn B-Bäume haben normalerweise eine Tiefe von etwa 2 bis 4 Stufen. Ändert sich nun ein solcher speicherresistenter Block, so wird er abgespeichert. Eine andere Möglichkeit ist, daß in einem geänderten Block ein Flag gesetzt wird, welches aussagt, daß der Block verändert wurde. Am Ende des Programms werden dann alle Blöcke abgespeichert, bei denen oder für die ein entsprechendes Flag gesetzt ist.

Mehrdeutige Schlüssel

Bayer-Bäume arbeiten normalerweise nur mit eindeutigen Schlüsseln.Für bestimmte Systeme (z.B. Adressverwaltung) ist es jedoch notwendig, daß ein Mehrfachauftreten des "gleichen" Schlüssels gewährleistet sein muß.
Dies kann man mit einem Trick erreichen :

Man setzt den Schlüssel aus zwei Teilen zusammen. Aus einem signifikanten Teil (z.B der Name) und einer Erweiterung (z.B. eine Zahl wird vom System bestimmt). Dadurch hat man physikalisch eindeutige und logisch mehrdeutige Schlüssel. Wird nun ein Schlüssel gesucht, so wird die Erweiterung auf "0" gesetzt und die Suchprozedur gestartet. Wurde ein Datensatz gefunden, so wird seine Erweiterung entsprechend verändert (z.B. inkrementieren) und mit dem so erzeugten Schlüssel die Prozedur wieder aufgerufen. Dieser Vorgang wiederholt sich solange, bis kein Eintrag mehr gefunden wird. Nimmt man als Erweiterung z.B. ein Integerzahl von 2 Byte, so kann man dadurch 256 * 256 = 65536 Datensätze unterscheiden.

Reorganisation

Eine Möglichkeit, um die Reorganisation von B-Bäumen durchzuführen, ist beim Vater die Pointer auf die Söhne und bei den Söhnen Pointer auf den Vater zu speichern. Dadurch entsteht jedoch ein erhebliches Problem :

Wird ein Nichtblatt gesplittet, so wird die Hälfte des Inhalts in einen anderen, neu erzeugten Knoten verlegt (neuer physk. und log. Offset). Die Vaterpointer der verlegten Söhne, des neuentstandenen Vaters, zeigen aber immer noch auf den alten Knoten (das äquivalente Problem entsteht natürlich auch beim Mischen). Diese Vaterpointer müssen also alle geändert werden, was bei k = 100 ein erheblicher Aufwand ist.



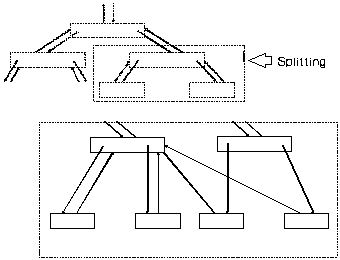
Die Söhne selbst befinden sich immernoch an der gleichen physikalischen Position, denn es wurde ja nur etwas im Vater der Söhne geändert. Die Reorganisation muß also nur die Stufe (und dort nur die entsprechenden Knoten), im Teilbaum unter dem Vaterknoten betrachten, die direkt darunter liegt. Diese Reorganisation pflanzt sich also nicht bis zu den Blättern fort.



Lösung: Bei B-Bäumen arbeitet man ohne Rückwärtsverkettung. Beim Durch suchen des Baumes von der Wurzel her merkt man sich alle Offsets der dabei durchlaufenen Knoten (z.B auf einem Stack). Muß jetzt eine Reor ganisation durchgeführt werden, so braucht man sich nicht anhand der Pointer vom Sohn zu Vater durch den Baum zu "hangeln" (Hintergrund speicherzugriffe), denn die benötigten Offsetadressen befinden sich schon im Hauptspeicher.